Sutton & Barto summary chap 02 - Multi-armed bandits

This post is part of the Sutton & Barto summary series.

• 2.1. A $k$-armed bandit problem
• 2.2. Action-value methods
• 2.3. The 10-armed testbed
• 2.4. Incremental implementation
• 2.5. Tracking a non-stationary problem
• 2.6. Optimistic initial values
• 2.7. Upper-Confidence-Bound (UCB) Action Selection
• 2.8. Gradient Bandit Algorithms
• 2.9. Associative search (contextual bandits)
• 2.10. Summary

In this chapter we study the evaluative aspect of reinforcement learning.

• Evaluative feedback: indicates how good the action taken was. Used in reinforcement learning.
• Instructive feedback: give the correct answer. Used in supervised learning.

Evaluative feedback $\rightarrow$ Need active exploration
The k-armed bandit problem is a good framework to learn about this evaluative feedback in a simplified setting that does not involve learning in more than one situation (nonassociative setting)

2.1. A $k$-armed bandit problem

• extension of the bandit setting, inspired by slot machines that are sometimes called “one-armed bandits”. Here we have $k$ levers ($k$ arms).
• repeated choice among $k$ actions
• after each choice we receive a reward (chosen from a stationary distribution that depends on the action chosen)
• objective: maximize the total expected reward over some time period

Each of the $k$ actions has a mean reward that we call the value of the action (q-value).

• $A_t$: action selected at time step $t$
• $R_t$: corresponding reward
• $q_*(a)$: value of the action

$$q_*(a) \doteq \mathbb{E}[R_t | A_t = a]$$

If we knew the values of each action it would be trivial to solve the problem. But we don’t have them so we need estimates. We call $Q_t(a)$ the estimated value for action $a$ at time $t$.

• greedy action: take the action with the highest current estimate. That’s exploitation
• nongreedy actions allow us to explore and build better estimates

2.2. Action-value methods

= methods for computing our $Q_t(a)$ estimates. One natural way to do that is to average the rewards actually received (sample average):

$$Q_t(a) \doteq \frac{\text{sum of rewards when a taken prior to t}}{\text{number of times a taken prior to t}} = \frac{\sum_{i=1}^{t-1} R_i \cdot \mathbb{1}_{A_i = a}}{\sum_{i=1}^{t-1} \mathbb{1}_{A_i = a}}$$

As the denominator goes to infinity, by the law of large numbers $Q_t(a)$ converges to $q_*(a)$.

Now that we have an estimate, how do we use it to select actions?

Greedy action selection: $A_t \doteq \underset{a}{\mathrm{argmax}}\;Q_t(a)$

Alternative: $\varepsilon$-greedy action selection (behave greedily except for a small proportion $\varepsilon$ of the actions where we pick an action at random)

2.3. The 10-armed testbed

Test setup: set of 2000 10-armed bandits in which all of the 10 action values are selected according to a Gaussian with mean 0 and variance 1.
When testing a learning method, it selects an action $A_t$ and the reward is selected from a Gaussian with mean $q_*(A_t)$ and variance 1.

TL;DR : $\varepsilon$-greedy $>$ greedy

2.4. Incremental implementation

How can the computation of the $Q_t(a)$ estimates be done in a computationally effective manner?

For a single action, the estimate $Q_n$ of this action value after it has been selected $n-1$ times is:

$$Q_n = \frac{R_1 + R_2 + ... R_{n-1}}{n-1}$$

We’re not going to store all the values of $R$ and recompute the sum at every time step, so we’re going to use a better update rule, which is equivalent:

$$Q_{n+1} = Q_n + \frac{1}{n} \big[ R_n - Q_n\big]$$

general form:

$$NewEstimate \leftarrow OldEstimate + StepSize [Target - OldEstimate]$$

The expression $[Target - OldEstimate]$ is the error in the estimate.

2.5. Tracking a non-stationary problem

• Now the reward probabilities change over time
• We want to give more weight to the most recent rewards

One easy way to do it is to use a constant step size so $Q_{n+1}$ becomes a weighted average of past rewards and the initial estimate $Q_n$:

$$Q_{n+1} \doteq Q_n + \alpha \big[ R_n - Q_n\big]$$

Which is equivalent to:

$$Q_{n+1} = (1 - \alpha)^n Q_1 + \sum_{i=1}^n \alpha(1 - \alpha)^{n-i} R_i$$

• we call that a weighted average because the sum of the weights is 1
• the weight given to $R_i$ depends on how many rewards ago $(n-i)$ it was observed
• since $(1 - \alpha) < 1$, the weight given to $R_i$ decreases as the number of intervening rewards increases

2.6. Optimistic initial values

• a way to encourage exploration, which is effective in stationary problems
• select initial estimates to a high number (higher than the reward we can actually get in the environment) so that unexplored states have a higher value than explored ones and are selected more often

2.7. Upper-Confidence-Bound (UCB) Action Selection

• another way to tackle the exploration problem
• $\varepsilon$-greedy methods choose randomly the non-greedy actions
• maybe there is a better way to select those actions according to their potential of being optimal

$$A_t \doteq \underset{a}{\mathrm{argmax}}\;\bigg[Q_t(a) + c \sqrt{\frac{\mathrm{ln}\;t}{N_t(a)}}\bigg]$$

• $\mathrm{ln}\;t$ increases at each timestep
• $N_t(a)$ is the number of times action $a$ has been selected prior to time $t$, so it increases every time a is selected
• $c > 0$ is our confidence level that controls the degree of exploration

The square-root term is a measure of the uncertainty or variance in the estimate of $a$’s value. The quantity being max’ed over is thus a sort of upper bound on the possible true value of action $a$, with $c$ determining the confidence level.

• Each time $a$ is selected the uncertainty is reduced ($N_t(a)$ increments and the uncertainty term descreases)
• Each time another action is selected, $\mathrm{ln}\;t$ increases but not $N_t(a)$ so the uncertainty increases

2.8. Gradient Bandit Algorithms

• another way to select actions
• so far we estimate action values (q-values) and use these to select actions
• here we compute a numerical preference for each action $a$, which we denote $H_t(a)$
• we select the action with a softmax (introducing the $\pi_t(a)$ notation)

Algorithm based on stochastic gradient ascent: on each step, after selecting action $A_t$ and receiving reward $R_t$, the action preferences are updated by:

$$H_{t+1}(A_t) \doteq H_{t}(A_t) + \alpha (R_t - \bar{R_t}) \big(1 - \pi_t(A_t)\big)$$

and for all $a \neq A_t$:

$$H_{t+1}(a) \doteq H_{t}(a) + \alpha (R_t - \bar{R}_t) \pi_t(a)$$

• $\alpha < 0$ is the step size
• $\bar{R_t}$ is the average of all rewards up through and including time t

The $\bar{R_t}$ term serves as a baseline with which the reward is compared. If the reward is higher than the baseline, then the probability of taking $A_t$ in the future is increased, and if the reward is below the baseline, then the probability is decreased. The non-selected actions move in the opposite direction.

2.9. Associative search (contextual bandits)

• nonassociative tasks: no need to associate different actions with different situations
• extend the nonassociative bandit problem to the associative setting
• at each time step the bandit is different
• learn a different policy for different bandits
• it opens a whole set of problems and we will see some answers in the next chapter

2.10. Summary

• one key topic is balancing exploration and exploitation.
• Exploitation is straightforward: we select the action with the highest estimated value (we exploit our current knowledge)
• Exploration is trickier, and we have seen several ways to deal with it:
  • $\varepsilon$-greedy choose randomly
  • UCB favors the more uncertain actions
  • gradient bandit estimate a preference instead of action values

Which one is best (evaluated on the 10 armed testbed)?

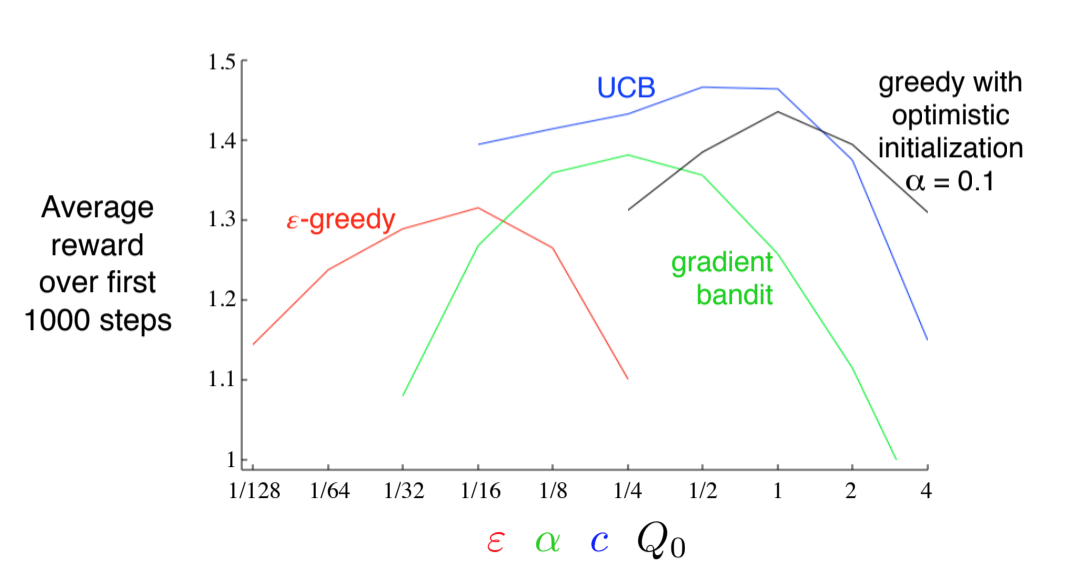Fig 2.1. Evaluation of several exploration methods on the 10-armed testbed